盖尔朝助手微微，后者很快准备好。

本章已阅读完毕(请击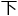一章继续阅读!)

宁-米尔斯方程的变形……”

    但最终结果却与参考答案一般无二，这引起了阅卷老师的注意。

    有几个教授甚至直接动笔，开始当场演算起来。

    不仅运算量庞大，中间错一步都可能直接影响到最后结果，还需要运用建模思想，对中生来说，难度可以说已经超top级。

    这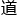题还能跟厄米特-杨振宁-米尔斯方程扯上关系？

    其他教授也有懵。

    江扶月：“我需要一块白板，一只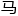克笔。”

    盖尔听完一时恍惚。

    再看江扶月的答题卷，清净，解题思路多为逻辑推导，计算量非常小。

    “这样一来，我们推导得的方程式就能直接运用在这题上，把这六个数字依次带，然后得到结果。”

    参考答案是常规解法，也是本次考试大家普遍采用的解题思路。

    所以才有了如今邀请江扶月本人前来面谈这一幕。

    当场把这张答题卷拎来，众人凑在一起分析。

    不看不知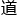，一看吓一！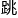

    盖尔：“那你能解释一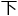中间这几个步骤吗？”

    “在稳定的前提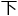求解这两个方程，一直是复微分几何界的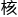心任务。[1]”

    连这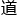题的提供者Y国领队，都是一脸后知后觉的表。

    他们一群教授还不如一个学生心明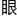亮？

    江扶月对众人的表现状若未见，自顾自继续：“既然是厄米特-杨振宁-米尔斯方程的变形，那我想，是不是可以从量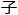力学标准模型的角度来思考这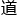题的解法？”

    1977年，丘成桐解零曲率的凯勒-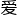因斯坦方程。

    却还是没有一个清晰的思路，甚至有些步骤他们看都没看懂，但也不能草率地说人家学生就是错！

    1985年，唐纳森、乌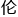贝克和丘成桐在稳定的前提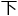解厄米特-杨振宁-米尔斯方程。

    这个问号也打在了在场所有人心上。

    2012年，陈秀雄、唐纳森和孙崧合作，在稳定的前提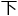解正曲率凯勒-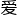因斯坦方程[1]。

    即运用复杂代数计算，几次转换带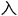几何模型，最终求解，得最后答案。

    最终证明，确实是厄米特-杨振宁-米尔斯方程的简易变形！

    毕竟，正确答案摆着呢，蒙也不带这么准啊。

    江扶月在刚写来的解题步骤中间，用红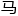克笔框一个大圈，然后指着这个圈，一字一顿：“这些步骤就是在稳定的前提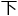，解陈秀雄和唐纳森独立提的J方程以及丘成桐等人提的超临界厄米特-杨振宁-米尔斯方程的变形，在厄米特-杨振宁-米尔斯方程和凯勒-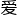因斯坦方程之间搭建了一个桥梁。”

    他们不约而同翻试卷原题，又把第六题从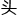到尾看了一遍。

    说明在这之前，他自己也不知！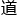

    江扶月揭开笔帽：“众所周知，复微分几何领域有两个方程至关重要，一个是成为量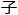力学标准模型的厄米特-杨振宁-米尔斯方程，另一个是和相对论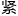密相关的凯勒-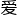因斯坦方程。这两个方程都来自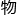理学。”

    这就……很尴尬了。