
 繁体
繁体
第200章 弦月之距【求月票】(2/2)
热门小说推荐
最近更新小说
这便是说,当直角三角形的两条直角边分别为3(勾)和4(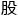 )时,径隅(弦)则为5,后世人们就简单地把这个定理说成“勾三
)时,径隅(弦)则为5,后世人们就简单地把这个定理说成“勾三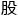 四弦五”,
四弦五”,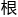 据该典故也称勾
据该典故也称勾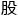 定理为商
定理为商 定理。
定理。
“是不难,我也没说过测算太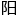 有多难。”
有多难。”
柴车怼了怼郭琎。
姜星火不打算绕圈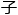 ,直白
,直白 :“刚才的等比例放大法。”
:“刚才的等比例放大法。”
月亮————太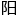
不过看着银币对准太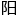 ,开始反光,三人倒也明白了姜星火的意思。
,开始反光,三人倒也明白了姜星火的意思。
老少三人齐齐望去。
“那勾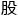 定理跟测算我们和太
定理跟测算我们和太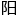 的距离,到底有什么关系呢?”
的距离,到底有什么关系呢?”
“啊,对对对!”
“殿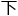 ,小臣倒是有个想法。”柴车忽然
,小臣倒是有个想法。”柴车忽然 。
。
没办法,数学这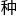 东西,不会就是真的不会。
东西,不会就是真的不会。
——————
姜星火提醒 :“
:“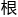 据地球直径,来算月亮直径,
据地球直径,来算月亮直径,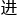 而推导太
而推导太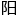 直径。”
直径。”
卓老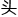 的
的 神开始变得有些茫然。
神开始变得有些茫然。
“弦月的时候!”
“而我们只需知 地球上的
地球上的 影区
影区 度,月亮的直径
度,月亮的直径 度,就可以等比例放大
度,就可以等比例放大 来!”
来!”
“月 。”
。”
这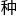 可以说是“手摘日月”的测算方式,显然还是过于超前了
可以说是“手摘日月”的测算方式,显然还是过于超前了
“那么从地球上看,太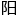 、月亮的大小基本相同,也就说明从地球看月亮和看太
、月亮的大小基本相同,也就说明从地球看月亮和看太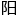 的视角是一样的所以,既然勾
的视角是一样的所以,既然勾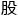 定理知
定理知 了太
了太 到地球的距离大约是月亮到地球的距离的几倍,那么也就能等比例推测
到地球的距离大约是月亮到地球的距离的几倍,那么也就能等比例推测 ,太
,太 直径是月亮直径的几倍,用很基础的相似三角形的比例关系就可以算
直径是月亮直径的几倍,用很基础的相似三角形的比例关系就可以算 来。”
来。”
闻言,三人再看着地面上的图案,刹那间竟然觉得其中仿佛蕴 了可以摘星拿月的天地至理一般。
了可以摘星拿月的天地至理一般。
“因为三者一条线的时候,也就是日全 的时候,月亮能几乎完
的时候,月亮能几乎完 挡住太
挡住太 。”
。”
卓老 兴致
兴致
 地指着地面上画的地球、月亮、太
地指着地面上画的地球、月亮、太 说
说 。
。
“地月直径比例,怎么算?”
卓老 反应了过来。
反应了过来。
毕竟,柴车也不是专门学天文和数术的,所以说,也只是灵光一闪,有这么一个想法,其他
 怎么算,就不太清楚了。
怎么算,就不太清楚了。
卓敬抬 看了一
看了一 姜星火,心中暗叹:“果真有通天彻地的能耐,
姜星火,心中暗叹:“果真有通天彻地的能耐, 衍所言,竟然非虚!”
衍所言,竟然非虚!”
勾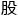 定理,只能把三个边和三个角给导
定理,只能把三个边和三个角给导 来,后面没路了啊!
来,后面没路了啊!
“这怎么等比例放大?”朱 煦清澈的
煦清澈的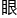 神里满是愚蠢。
神里满是愚蠢。
“肯定不是。”卓敬摇了摇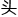 。
。
朱 煦作为姜星火的开山大弟
煦作为姜星火的开山大弟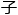 ,知
,知 自己在姜先生心中的固有印象,所以充分发挥了不懂就问的优良学风。
自己在姜先生心中的固有印象,所以充分发挥了不懂就问的优良学风。
还真别说,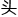 脑风暴一
脑风暴一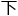 ,就是比一个人苦思冥想好得多。
,就是比一个人苦思冥想好得多。
朱 炽忙
炽忙 。
。
换句话说,在月亮表面反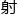 的太
的太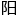 光,与地球之间,呈现了直角!
光,与地球之间,呈现了直角!
卓老 越说越兴奋,甚至有些手舞足蹈了起来。
越说越兴奋,甚至有些手舞足蹈了起来。
姜星火又在地面上开始画画了,他一边画一边说 :“勾
:“勾 定理算
定理算 来了地球、月亮、太
来了地球、月亮、太 三者的距离比例(假设地月距离为1单位)和角度,那么可以用等比例放大,来推算太
三者的距离比例(假设地月距离为1单位)和角度,那么可以用等比例放大,来推算太 直径。”
直径。”
指鹿为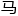 了属于是。
了属于是。
“如何算?”
“你说来听听。”
闻言,朱 炽倒也没有为难他,毕竟朱
炽倒也没有为难他,毕竟朱 炽也没指望从这两个小吏
炽也没指望从这两个小吏 中能得到答案,都是寻常读书人。
中能得到答案,都是寻常读书人。
姜星火摆 着手里的银币,调整着位置。
着手里的银币,调整着位置。
“所以接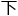 里,因为郭守敬已经算
里,因为郭守敬已经算 来了地球的半径、直径,我们只需要算地月直径比例,得到了月球的直径,就能通过倒推
来了地球的半径、直径,我们只需要算地月直径比例,得到了月球的直径,就能通过倒推 来上一步的太
来上一步的太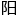 直径?”
直径?”
没办法,几何这东西有的时候是真的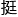 好用的。
好用的。
30天,就是一个“月”。
“有关系啊。”
画完,姜星火解释起了原理。
“那我问你们,请问什么时候,月亮、太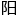 、地球三者,才会如上面画的图一样,以月亮为一
、地球三者,才会如上面画的图一样,以月亮为一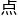 ,与太
,与太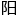 和地球同时呈直线,构成一个直角呢?”
和地球同时呈直线,构成一个直角呢?”
密室里,朱 炽开始搞“三个臭裨将
炽开始搞“三个臭裨将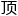 个诸葛亮”了,他看向了郭琎和柴车。
个诸葛亮”了,他看向了郭琎和柴车。
地球—月亮—太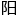
说会正题,所谓上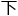 弦月,从月相上判断,还能看到的月亮完整边沿弧线当
弦月,从月相上判断,还能看到的月亮完整边沿弧线当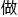 弓臂,在
弓臂,在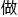 一条虚线连接弧线两端,想象成弓弦,弦在月亮上侧为上弦月,在
一条虚线连接弧线两端,想象成弓弦,弦在月亮上侧为上弦月,在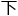 侧为
侧为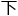 弦月。
弦月。
“没错。”
说罢,姜星火又拿 了他的经典教
了他的经典教 。
。
所以,朱 炽把希冀的目光,望向了那面饱经沧桑的扩音墙
炽把希冀的目光,望向了那面饱经沧桑的扩音墙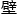 。
。
“这两个时间的比例,也就是月亮直径,与月亮所经过地球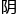 影区的比例。”
影区的比例。”
本章已阅读完毕(请 击
击 一章继续阅读!)
一章继续阅读!)
“然后怎么算?”
正是因为想明白了这个 理,卓老
理,卓老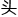 才兴奋地
才兴奋地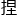 断了一个宝贵的、所剩无几的胡须。
断了一个宝贵的、所剩无几的胡须。