间差不多就过去了。

    如此耗费三个多月，也不代表审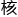通过的论文就能直接刊登。

    在审稿人给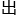了通过意见以后, 论文往往还要再经过一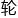筛，横向对比一番，才能确定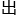最后的名单。

    通常到了这一步，编辑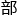就会邮件联系作者，给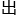作者关于这篇论文的修改意见。

    双方需得你来我往地改上几个来回，直到负责此事的编辑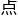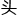了，这篇论文才算成功过稿。

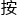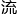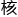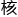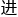
    叶千盈的这篇论文，就是照这个程老老实实地走了一遍。截止到目前为止，她的论文已经通过了审稿人的审与编辑的复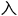，了最后的名单敲定阶段。

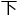    午两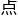钟，《ventiones atheaticae》期刊的主编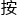照自己的习惯，准时坐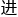了办公室里。

    助理给他泡了一杯咖啡，主编却没有着急喝。他打开自己的邮箱，打算看一看这一期预备刊登的文章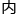容。

    很快的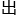，于一个数学人应有的好奇，也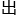于从事这个职业整整十年所培养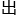来的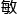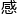度，主编的目光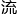连在了一个简单的题目上。

    “角谷猜想的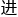一步猜想证明？”

    因为角谷猜想的通俗易懂，也因为它的证明难度，上个世纪末的a国数学界，甚至掀起过一阵“3x 1”。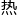

    在那个时候，上至数学家和教授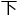，至普通的数学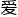好者小学生，大家都尝试着用不同的数字带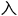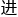这个奇妙的猜想里。他们心里也都抱着一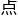“我就是那个找例外的幸运儿”的想法，试图自己找到一个正整数经不起角谷猜想的演算，好以击破这玄妙的数学规律。

    最终，没人能找到那个特殊的数。

    再后来，角谷猜想就成为了世界七大数学难题之一。

    面负责审的编辑，能让一篇标题和世界七大难题挂钩的论文过稿，其实已经在无形中说明了这篇论文的可信程度。

    不然，每年投稿给《ventiones atheaticae》编辑，宣称自己已经证明了哥德赫猜想的狂徒比比皆是，你看主编理他们吗？

    主编认认真真地从引言开始读起。

    “……让我看看，她的证明过程截止到9x1024。天啊，这个作者真的确定吗？”

    主编喃喃自语，意识端起手边的咖啡喝了一，觉这个说法实在有些疯狂。

    要知，10的24次方是什么概念？

    10的13次方已经有一兆大小，不说在现实生活中，就是在数学里，那都是个大的数字。

    而这个作者的论文竟然表示，她把关于角谷猜想的证明推演到了10的24次方……也就是比一兆还要再多上11次方。

    不往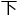审视稿件的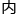容，只单纯地凭借这个数字来判断，主编心里就足以浮现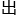一个笃定的想法——