安宴一边讲解论文，一边看着大家的表，发现

    2∪…∪Ws构成空间， 且不妨设W糉n.由于任一线空间的空间都是一个齐次线方程组的解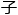空间， 对每个i (i=1， 2， …， s) ， 不妨设Wi均为n-1维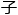空间 (不然将Wi扩大即可) ， 设以Wi为解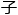空间的线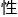方程分别为ai1x1 ai2x2 … ainxn=0， i=1， 2， …， s.

    ai1x1 ai2x2 … ainxn=0， i=1， 2， …， s.

    令fi=ai1x1 ai2x2 … ainxn， 则fi=0 (即该超平面的定义方程) 在几何上表示由多项式fi定义的仿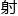簇Vi.由于对于每个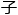空间， 存在一个包它的超平面， 从而对于每个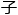空间Wi， 存在一个包它的仿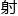簇Vi， 其中i取值均为1， 2， …，……①】

    对于每个i， ai1x1 ai2x2 … ainxn=0表示一个超平面.

本章已阅读完毕(请击一章继续阅读!)

厅之前，其实还不太张。但是看见面全都是大佬，一就张了起来。

    另一方面， 取 (a1， a2， …， an) ∈V (fpgq) ， 如果该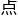在V中， 那么就完成了证明.如果该不在V中， 那么对某个p0， 有fp0 (a1， a2， …， an) ≠0.又因为fp0gq对所有的q， 在 (a1， a2， …， an) 都等于0， 那么gq一定在这个为0， 这就证明了 (a1， a2， …， an) ∈W.于是得到V (fpgq) 糣∪W.

    【……

    综上有V∪W=V (fpgq) .因此V∪W也是仿簇……

    安宴一气，将准备好的资料放在电脑上说，“我现在开始讲解关于阿贝尔簇算术质和解析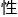质之间的联系问题。”

    对每一个i， fi (T) 最多有n-1个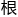， 故这些多项式最多有s (n-1) 个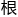.而F中有无限多个元素， 因此存在t∈F， 使得fi (t) ≠0， 即ai1 ai2t ai3t2 … aint n-1≠0， i=1， 2， …， s.

    由这些方程导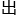关于未定元T的多项式fi (T) =ai1 ai2T ai3T2 … ainTn-1， i=1， 2， …， s.

    设βj= (1， tj， tj2， …， tjn-1) T， j=0， 1， 2， …， n-1， 其中tj (j=0， 1， 2， …， n-1) 满足……

    假设V=V (f1， f2， …， fk) ， W=V (g1， g2， …， gl) ， 其中k和l为正整数.则有V∪W=V (fpgq:1≤p≤k， 1≤q≤l) .一方面， 如果 (a1， a2， …， an) ∈V， 那么所有的fp在这一为0， 也就蕴着所有的fpgq在 (a1， a2， …， an) 也等于0.因此V糣 (fpgq) .类似地， 有W糣 (fpgq) .这就证明了V∪W糣 (fpgq) .

    率先说话的是德利涅教授，“安，不需要张，你现在只需要好好答辩就行。”