嘿嘿……”

    “哈哈……”

    整个教室的气氛一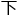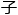就松弛了起来，万教授趁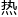打铁继续说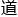，“原本我是打算今天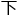午测试的，但是没有想到还有五个人没有到。那么就先给你们说说微积分吧，微积分主要分为微分学和积分学……咱们这里，把微积分学得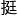好的，迄今为止我能够看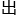来的也就是王云同学一个，不过大家也别气馁，你们数学基础知识已经很扎实。能够从几万名中生中脱颖而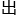，你们觉得自己连一个微积分都学不好吗？”

    “首先，我们讲解一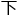微分。”

    “微分（Differentiation）在数学中的定义：由函数B=f(A)，得到A、B两个数集，在A中当dx靠近自己时，函数在dx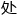的极限叫作函数在dx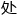的微分。”万教授看着五个学生说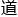，“我这么说，你们是不是觉得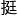简单的？”

    几位学生微微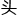，万教授继续说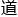，“这只是微分的基本概念，接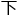来我要说的便是一元型。”

    【设函数y = f(x)在x的邻域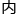有定义，x及x   Δx在此区间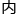。如果函数的增量Δy = f(x   Δx) - f(x)可表示为Δy = AΔx   o(Δx)，而o(Δx)是比Δx阶的无穷小那么称函数f(x)在x是可微的，且AΔx称作函数在x相应于因变量增量Δy的微分，记作dy，即dy = AΔx。】

    【自变量x的增量Δx称为自变量的微分，记作dx，即dx = Δx。于是函数y = f(x)的微分又可记作dy = f\'(x)dx。】

    【当自变量X改变为X △X时，相应地函数值由f(X)改变为f(X △X)，如果存在一个与△X无关的常数A，使f(X △X)-f(X)和A·△X之差是△X→0关于△X的阶无穷小量，则称A·△X是f(X)在X的微分，记为dy，并称f(X)在X可微。一元微积分中，可微可导等价。记A·△X=dy，则dy=f′(X)dX。】

    【例如：d(sinX)=cosXdX】

    “现在呢？”万教授一边在黑板上写着公式，一边看着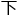面的表。看见大家还不算是脸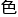太差，于是他转过来，将粉笔放在讲台上说，“我知，大家对于微分应该都有些了解。那么——”

    万教授拿起粉笔在黑板上写了一题目——

    【求由方程2y－x＝(x－y)ln（x－y）所确定的函数y＝y(x)的微分dy】

    “？？？”这一大家都给懵，他们囫囵吞枣的看了一遍微积分，刚才万教授说的基础知识他们勉勉还算是能够听懂，真要让他们题，立就给懵了。