Bain教授听见王云的话，转过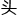来看向Witten教授说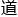，“Witten，老伙计，你果然收了一个好徒弟。”

    “看来你是看懂了。”Bain教授颇为有些欣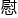，“没想到你对于泛函分析也还是有些研究的，那么接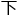来——”

    王云默默地站在Witten教授的边，没有继续说话。听着他们谈论量场论和泛函分析，原本听得还是津津有味的。没想到，Bain教授看向王云笑眯眯的说，“我听说你对于非线偏微分方程研究得不错？”

本章已阅读完毕(请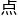击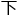一章继续阅读!)

    “Bain教授对于你想要解开N-S方程非常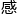兴趣。”Witten教授看向王云，招了招手说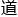，“王，你已经见过Bain教授了对吧？”

    定理A[6] 假设条件(a)和(b)均成立，对于(t，x)∈J×Y有‖f(t，x)‖≤g(t，‖x‖)，其中g∈C[R ×R ，R ]同时关于第二变量为非减函数。如果初值问题

    “没错。”王云微笑着说，“Bain教授我见过，就是在学术报告会的时候就已经见过了。”说是这么说，王云也知，这只是Witten教授在客气而已。Witten教授应该不会忘记，上次的学术报告会，Bain教授当着他的面挖自己的事吧？

    u′=g(t，u)，u(t0)=u0>0(2.2)的最大解u(t，t0，u0)在J上全局存在，于是对于每个x0∈X且‖x0‖≤u0，初值问题(2.1)在J上都存在一个全局解。①】

    【x′=f(t，x)，x(t0)=x0 (2.1)的解的全局存在，其中f:[t0，T]×X→X，T可以取正无穷，f是一个连续函数，同时记J=[t0，T]。为了方便，我们作以假设(a)f∈C[J×X，X];(b)对于(t0，x0)∈J×X上的每个初始数据，初值问题(2.1)存在一个局解。

    王云笑着说，“我原本也是想要与Witten教授一同研究希尔伯特猜想的，不过我觉得在普林斯顿待了半年的时间，或许能够尝试着解开N-S方程，倘若是解不开，在跟着Witten教授一起研究也不会太迟。”

    “虽然我研究的是泛函分析领域，这一分，相信你的导师Witten教授多少也是有些心得的，王，你看这个——”说这里的时候Bain教授拿着笔在小黑板上写了起来——

    Bain教授突如其来的询问，让王云有些反应不过来，好半天之后，这才讷讷地，“算是有些一些研究。”

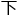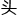    王云挑动了一眉，这是——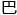拿赫空间中非线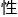常微分方程边界问题吧？唔，他对于泛函分析这方面了解得不太多，正好Bain教授又是其中的手，或者是说，是全球最尖的一批泛函分析领域的大师。

    Bain教授打量着王云，“王，你可真是让我觉很惊讶，没有想到你解开了角谷猜想之后，竟然会选择N-S方程作为博士课题研究。我以为你依旧还是往微分拓扑学发展，或者和你的导师一起研究希尔伯特猜想。”

    为了证明这一分的主要结果，首先涉及到初值问题(2.1)存在一个全局解的定理和面的两个相关引理。