
 繁体
繁体
分卷阅读113(2/2)
热门小说推荐
最近更新小说
本章已阅读完毕(请 击
击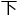 一章继续阅读!)
一章继续阅读!)
3个人互相都不认识,则3个 互相连接的线段都是红
互相连接的线段都是红 ,可以形成一个红
,可以形成一个红 三角形。那么题目就转化为了简单的数学图形题——有没有可能绿
三角形。那么题目就转化为了简单的数学图形题——有没有可能绿 三角形和红
三角形和红 三角形都不
三角形都不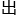 现?如果答案是肯定的,那么那句话就是错的,如果绿
现?如果答案是肯定的,那么那句话就是错的,如果绿 三角形或者红
三角形或者红 三角形单独
三角形单独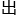 现或同时
现或同时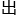 现,那么那句话就是对的。
现,那么那句话就是对的。
当然,有这个好 的,只有必须回答问题才能抓住的岩
的,只有必须回答问题才能抓住的岩 。谈苏一开始手握的岩
。谈苏一开始手握的岩 ,没这个功能,她只能靠自己的臂力
,没这个功能,她只能靠自己的臂力 抓着它,没一会儿就觉得手指酸痛。
抓着它,没一会儿就觉得手指酸痛。
不会……被 住就松不了了吧?
住就松不了了吧?
谈苏试着松开手指,担忧中被牢牢 住的画面并没有
住的画面并没有 现,她轻轻松松就将岩
现,她轻轻松松就将岩 松开了。她微微皱起眉,又尝试了几次,这才
松开了。她微微皱起眉,又尝试了几次,这才 明白了规律——当她的手指在岩
明白了规律——当她的手指在岩 上稍稍用力时,那
上稍稍用力时,那
 大的
大的 力就会将她牢牢地
力就会将她牢牢地 在井
在井 上,甚至她松开了另一手
上,甚至她松开了另一手 抓的岩
抓的岩 ,只靠这一只手支撑整个
,只靠这一只手支撑整个
 的重量,也完全不会掉
的重量,也完全不会掉 去。而当她的手指完全放松时,那
去。而当她的手指完全放松时,那
 力就消失了。也就是说,只要她
力就消失了。也就是说,只要她 抓这个岩
抓这个岩 ,
,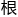 本不用担心一会儿爬累了会掉
本不用担心一会儿爬累了会掉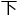 去了。
去了。
因此,经过推导得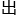 的结论是,绿
的结论是,绿 三角形和红
三角形和红 三角形至少有一个会
三角形至少有一个会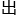 现,回归到原题中,绿
现,回归到原题中,绿 三角形代表“有3个人互相认识”,红
三角形代表“有3个人互相认识”,红 三角形代表“有3个人互相都不认识”,也就是说,“至少有3个人互相认识”和“至少有3个人互相都不认识”,这两句话至少有一句是正确的,即,原命题正确。
三角形代表“有3个人互相都不认识”,也就是说,“至少有3个人互相认识”和“至少有3个人互相都不认识”,这两句话至少有一句是正确的,即,原命题正确。
谈苏脸 微变。
微变。
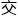 换一
换一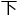 颜
颜 ,即将3条红
,即将3条红 ,2条绿
,2条绿 作为前提
作为前提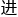 行推导的过程完全类似,结论也是一样的。如果颜
行推导的过程完全类似,结论也是一样的。如果颜 分
分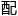 是4和1或者5和0的
是4和1或者5和0的 况,也是用类似的推导方法,得
况,也是用类似的推导方法,得 相似的结论。
相似的结论。
一个 可以画
可以画 5条线段,而线段只有两
5条线段,而线段只有两 颜
颜 ,那么从一个
,那么从一个
 发的5条线段,最均匀的分
发的5条线段,最均匀的分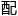 是2和3。假设从一
是2和3。假设从一 A
A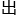 发的线段中有3条绿
发的线段中有3条绿 ,2条红
,2条红 ,而那3条绿
,而那3条绿 连接的
连接的 分别是
分别是 B,
B, C,
C, D,这3个
D,这3个 之间如果有一条是绿
之间如果有一条是绿 ,则会与跟A相连的绿
,则会与跟A相连的绿 线段一起形成一个绿
线段一起形成一个绿 三角形;而如果这3个
三角形;而如果这3个 之间一条绿
之间一条绿 都没有,由于只有两
都没有,由于只有两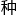 颜
颜 ,不是绿
,不是绿 就是红
就是红 ,那么这3个
,那么这3个 之间就会形成一个红
之间就会形成一个红 三角形。综上所述,至少会有一个红
三角形。综上所述,至少会有一个红 三角形或者一个绿
三角形或者一个绿 三角形。
三角形。
之后,谈苏又试着查看左右附近的岩 ,有些是需要回答问题的,另一些则不需要。不同类型的岩
,有些是需要回答问题的,另一些则不需要。不同类型的岩 分布得很有规律,想要不靠有
分布得很有规律,想要不靠有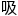 力的岩
力的岩 爬上去,或者只靠有
爬上去,或者只靠有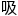 力的岩
力的岩 爬上去,又或者混合着爬,都是可以办到的。如果说她够不着的上方,岩
爬上去,又或者混合着爬,都是可以办到的。如果说她够不着的上方,岩 分布方式也跟
分布方式也跟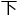 面的一样,那么就足以说明,这一主线任务的灵活
面的一样,那么就足以说明,这一主线任务的灵活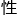 很
很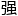 。回答不了问题的人,可以只抓着不用回答问题的岩
。回答不了问题的人,可以只抓着不用回答问题的岩 向上爬,避开必须回答问题这一考验脑
向上爬,避开必须回答问题这一考验脑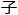 的障
的障
虽然解题步骤需要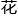 费一定的时间,但谈苏稍稍回忆就记起了答案,所以看清楚题目之后立刻
费一定的时间,但谈苏稍稍回忆就记起了答案,所以看清楚题目之后立刻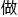
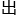 了回答。题目的
了回答。题目的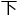 方有两个
方有两个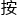 钮,一个是“正确”,另一个是“错误”,她
钮,一个是“正确”,另一个是“错误”,她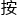
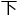 了正确的
了正确的 钮,屏幕消失,而原本灰扑扑的岩
钮,屏幕消失,而原本灰扑扑的岩 变成了浅绿
变成了浅绿 。谈苏忙将手放了上去,
。谈苏忙将手放了上去,
 抓住它。然而让她吃惊的是,那岩
抓住它。然而让她吃惊的是,那岩 上竟然传来一
上竟然传来一
 力,将她牢牢地
力,将她牢牢地 在岩
在岩 上。
上。