钱老师说话慢悠悠：“ IMO历史上有著名的题目, 叫传奇的第6题, 不知你听说过没有？”

    许晨在旁边，觉钱老师是个实在人。这题目的确简单，连他都听明白是什么意思了。

    “韦达跃包两个分，一个是韦达定理，另一个是无穷递降法。”

    这宋楠楠还真没听说过。她搞数学竞赛也就一年，严格来讲, 还没有摸到奥数的边。

    “题目听着简单的，假设正整数a、b, 满足ab   1可以整除a^2   b^2，证明(a^2   b^2) / (ab   1) 是某个整数的平方。”

本章已阅读完毕(请击一章继续阅读!)

    “当然。”钱老师脸上的笑容更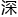了，“不然的话，我们也不知这题目呀。”

    这跟拿考题去欺负小学生有什么区别呀？

    钱老师愈发笑得舒坦：“他们本来以为没有学生能够解答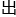来，可是那一届数学竞赛有11个考生拿到了满分。”

    宋楠楠有些懵，后者她知，无穷递减法是一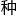反证法，学数学归纳法的时候会谈到反证法。

    钱老师笑得更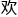畅了：“你还真是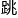跃，真算起来，无穷

    许晨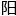听到这儿已经惊呼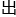声：“妈呀，这是人的题目吗？最厉害的数学家都解不来。啊，你说它是第6题，难不成它真放到试卷上了？”

    宋楠楠也目瞪呆：“他们是怎么来的？”

    虽然他不知该怎么证明。

上那些培训班的更加不是奥数，不过是提前学习而已。小学学初中的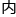容，初中学中, 中学大学。这就抓住了奥数的妙之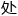吗？没意义, 毫无意义。奥数的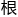本意义是夯实基础，灵活运用。”

    真让她去解什么千禧年十大难题，发明某个公式定理吗？开什么玩笑，大白天的就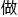梦。

    简单儿讲，假设方程式有解，且最小解为x，那么从x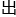发，试着推导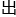另一个更小的解y。如果这个推导成功，那么就跟“x为最小解”的假设相矛盾，从而证明此方程式无解。

    可是韦达定理又是什么？

    钱老师笑了起来，原本因为生活沧桑而过分衰老的容颜，瞬间居然显了孩气。

    钱老师意味：“其中公认最巧妙直接碾压了标准答案的解法运用的就是中学数学容，韦达跃。”

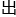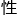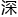
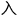
    虽然说天才年年有，数学界是公认天才的领域。但奥数组委会的专家本就是天才中的天才，他们掌握知识的全面与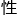，肯定能够碾压学生。

    宋楠楠有些懵，她还真不知什么是韦达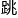跃。所以说，她自称奥数的门外汉，真不是谦虚。

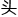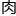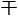    宋楠楠乖巧地，只等着钱老师说戏。理她都懂, 可问题是如果不学这些，她又能什么？

    他赞叹不已：“这就是这题的巧妙之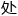啊，极度简单却又用意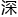远。你不知该怎么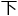手很正常。当年西德提供题目之后，拟题组委会的6位专家都没能解来，他们又向世界知名的4位数论专家求助，依然未果。”

    许晨受到了绝望，这个国际奥数该有多变态。负责题的老师自己都不会写，居然也好意思拿来。让学生坐这些数学家都是大学教授吧。可这个国际奥数竞赛面对的考生不是中学生吗？

    这是没办法的事，任何一个学科都有积累的过程。